A Sense of Doubt blog post #1601 - The Apollo Guidance Computer (and Bitcoin)

A Sense of Doubt blog post #1601 - The Apollo Guidance Computer (and Bitcoin)

Material will always present itself.

I was seeking a share for today, and I have not posted in some time about computers and coding. I am only interested in Bitcoin because I feel I should be. Mainly, I am sharing this post because I am interested in how it describes and explains the AGC -- Apollo Guidance Computer -- used in the Apollo missions. The 50th anniversary of Apollo 11 is this year and right about this time of the year (July 16th).

The Bitcoin experiment with this computer really tells the tale well on the ways in which Moore's Law has worked since the late 1960s to give us the technology we have today. The exponential curve of a doubling every 18-24 months over 50 years results in a difference, unsurprisingly, greater than the age of the universe. As you will, A LOT greater.

Here's the share.


FROM:

http://www.righto.com/2019/07/bitcoin-mining-on-apollo-guidance.html

Ken Shirriff's blog

Xerox Alto restoration, IC reverse engineering, chargers, and whatever

Bitcoin mining on an Apollo Guidance Computer: 10.3 seconds per hash

We've been restoring an Apollo Guidance Computer¹. Now that we have the world's only working AGC, I decided to write some code for it. Trying to mine Bitcoin on this 1960s computer seemed both pointless and anachronistic, so I had to give it a shot. Implementing the Bitcoin hash algorithm in assembly code on this 15-bit computer was challenging, but I got it to work. Unfortunately, the computer is so slow that it would take about a billion times the age of the universe to successfully mine a Bitcoin block.

The Apollo Guidance Computer powered up. The cover is off, showing the computer's purple wire-wrap wiring of the backplane. We built the interfaces that are plugged into the front of the computer. At the back, vintage core rope simulator boxes are visible in the core rope slots.

The Apollo Guidance Computer was developed in the 1960s for the Apollo missions to the Moon. Onboard the Apollo spacecraft, these computers provided guidance, navigation, and controlled the engines. In an era when most computers ranged from refrigerator-sized to room-sized, the Apollo Guidance Computer was small enough to fly in space. One of the very first computers to use integrated circuits, the AGC was 70 pounds and under a cubic foot in size.

The output from the Bitcoin mining program, displayed on the Display/Keyboard (DSKY). The display shows part of the Bitcoin hash in octal. The DSKY is a modern replica, hooked up to the genuine AGC.

The Apollo Guidance Computer also pushed the boundaries of software engineering under the leadership of Margaret Hamilton. It had a cutting-edge real-time operating system that supported multiple prioritized jobs² along with fault detection and handling. Much of the software was in assembly language but the AGC also had an interpreter designed for navigation algorithms. The interpreter implemented a virtual machine that provided vector and matrix arithmetic along with trigonometry and double- and triple-precision numbers.

How Bitcoin mining works

As the leading digital currency, Bitcoin has received a lot of attention in the past few years. The Bitcoin system can be thought of as a ledger that keeps track of who owns which Bitcoins, and allows them to be transferred from one person to another. The revolutionary feature of Bitcoin is there's no central machine or authority keeping track of things. Instead, the records are spread across thousands of machines on the Internet, and the system works with nobody in charge.

To ensure everyone agrees on which transactions are valid, Bitcoin uses a process called mining—about every 10 minutes a block of outstanding transactions is mined, which makes the block "official". Bitcoin mining is designed so it takes an insanely huge amount of computational effort to mine a block, so nobody can take over the mining process. Miners compete against each other, generating trillions and trillions of random "hashes" until someone finds a lucky one that starts with 18 zeros.³ This hash forms a successfully mined block, and then everyone moves on to the next block. The idea is that getting 18 zeros in a row randomly is extremely unlikely, so it takes a huge number of tries before someone succeeds. It's kind of like a lottery, where miners keep trying until someone "wins", but finding a valid hash is less likely than finding a single grain of sand out of all the sand on Earth.

Each time a block is successfully mined, new Bitcoins are created; currently, a successful miner gets 12.5 new Bitcoins (worth $140,000) as well as transaction fees. The possibility of receiving $140,000 every 10 minutes motivates miners to build datacenters full of specialized hardware using huge amounts of electricity.⁴

Structure of a Bitcoin block. The data in yellow is hashed to yield the block hash, which becomes the identifier for the block. The block is linked to the previous block by including the previous block's hash, forming the blockchain. The Merkle root is a hash of all the transactions in the block.

The diagram above shows what actually goes into a block that is mined. The yellow part is the block header (which gets hashed), and it is followed by the transactions that go into the block. Each block contains the hash of the previous block, causing all the blocks to be linked together forming the blockchain. On the right, you can see that the hash above was successful because it starts with lots of zeros.

To summarize the mining process: you collect new Bitcoin transactions and create a header as in the diagram above. You generate the cryptographic hash of the block. If by some incredible chance the result starts with 18 zeros you send the block into the Bitcoin network and "win" $140,000 in Bitcoin. Otherwise, you change the header slightly and try again as fast as possible. When someone else succeeds in mining the block, you start over from the new block and new transactions.⁵

The SHA-256 hash algorithm used by Bitcoin

Where do these hashes come from? Bitcoin mining is based on cryptography, with a "hash function" that converts a block of data into an essentially random hash value. The hash algorithm is designed to be simple to implement, but cryptographically secure: there's no known short cut to finding a successful hash other than trying zillions of hashes through brute force. In particular, Bitcoin uses a standard cryptographic hash function called SHA-256.⁶ This algorithm is so simple you can literally do it by hand, but it manages to scramble the data entirely unpredictably.

The SHA-256 algorithm can be described in about a page of pseudocode. It consists of a scrambling step called a "round", repeated 64 times. The diagram below shows one round, which takes eight 4-byte hash values, A through H, performs a few operations, and generates new values for A through H. As can be seen from the diagram, only A and E are changed in a round, while the others are just shifted over. Even so, after 64 rounds the input data will be completely scrambled, generating the unpredictable hash output.

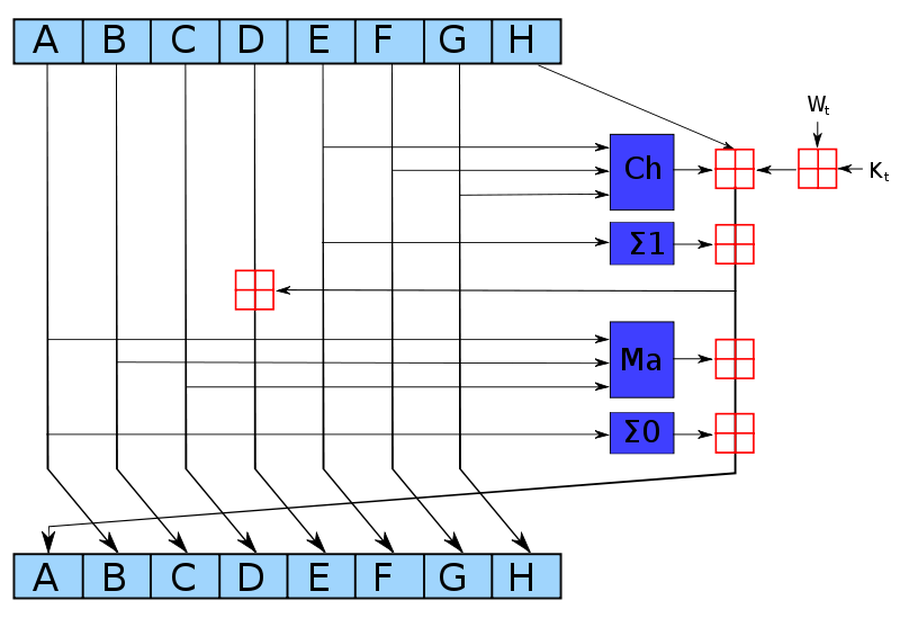This diagram shows the computations during one round of SHA-256. This process is repeated 64 times. Source: Wikipedia created by kockmeyer, CC BY-SA 3.0.

The operations in SHA-256 are simple bit operations. The red boxes above indicate 32-bit addition, generating new values for A and E. The Ch "choose" box chooses bits from F or G, based on the value of input E. The Σ "sum" boxes rotate and sum bits. The Ma "majority" box looks at the bits in each position of A, B, and C, and selects whichever value is in the majority. The K_t values are constants. The input data enters the algorithm through the W_t values. These operations can be easily implemented on a computer using simple arithmetic and logic operations.⁷ (The operations can also be easily implemented in a custom logic circuit, which is why Bitcoin mining chips are popular.)

The Apollo Guidance Computer's processor

A logic module from the Apollo Guidance Computer. The module consists of 120 integrated circuits, each one implementing two NOR gates. Photo courtesy of Mike Stewart.

The AGC doesn't have a microprocessor, as it was built years before microprocessors were developed. Instead, the processor is built from about 5600 NOR gates. These gates were combined to make circuits such as flip flops for registers, binary adders, control logic, and so forth. The AGC was one of the first computers to use integrated circuits; each integrated circuit held two NOR gates. The computer had 24 logic modules similar to the one below. Each logic module had 120 integrated circuits (240 NOR gates). For example, the registers and ALU were implemented with four modules, each implementing 4 bits of the processor.

The computer's architecture was unusual by modern standards: it used a 15-bit word, along with parity. (Back then, computers often had a word size that fit the application, not necessarily a power of 2.) The AGC had just 2K words of RAM, along with 36K words of ROM. Its ROM was constructed from core rope memory. (I wrote about the AGC's RAM core memory here and core rope here).

The Apollo Guidance Computer was slow even by 1960s standards; it could perform about 40,000 additions per second. (In the AGC's defense, this was an era when most computers ranged from refrigerator-sized to room-filling, so the AGC did well for its size.) The AGC's main strength was I/O: it had hundreds of I/O connections to provide real-time control of the spacecraft.

Implementing SHA-256 on the Apollo Guidance Computer

My implementation of the SHA-256 hash algorithm implementation follows the pseudocode pretty closely. I ran into some difficulties, though, since the AGC's instruction set lacks many features of modern computers. For instance, the AGC (like many 1960s computers) didn't have a stack, so you had to keep track of the return address for each subroutine call.

Another complication was that the SHA-256 algorithm uses 32-bit unsigned numbers, while the AGC used 15-bit signed numbers in obsolete 1's complement form, so even addition required some tricky code. To fit a 32-bit number into the AGC, I split each word into a 4-bit chunk and two 14-bit chunks. (I used 14-bit chunks and not 15-bit chunks because I needed to use unsigned arithmetic.)

The next issue was that the AGC has very limited memory. The AGC, like most computers of the 1960s, used magnetic core memory, storing each bit in a tiny magnetized ferrite ring. Since core memory was fairly bulky, the AGC had just 2K words (approximately 4K bytes) of RAM. The AGC's addressing scheme made things more complicated since you could only access 256 words unless you used an inconvenient bank switching mechanism. The problem is that the SHA-256 algorithm uses eight (32-bit) hash values, a 64-word message table, and 8 words of intermediate values. These three arrays alone used up 240 AGC words, leaving about 16 words for everything else (temporary values, subroutine return addresses, loop counters, pointers, etc.) I managed to get everything to fit in one bank by reusing these 16 words for multiple purposes, but I spent a lot of time debugging problems when a variable clobbered a location still in use.

For RAM, the Apollo Guidance Computer used this 2 kiloword core memory module.

Most modern computers have shift and rotate instructions to manipulate words, but the AGC instead used three special registers. Writing to a special register would cycle the value right one bit, shift the value right, or cycle the value left. The SHA-256 algorithm uses many 32-bit shifts and rotates, which I had to convert into loops using the 15-bit cycle register. The point is that a shift operation like x>>10 is trivial in C, but I needed to implement a whole subroutine to do it on the AGC.

Our Apollo Guidance Computer and replica DSKY. The computer's I/O connectors are visible at the front of the computer. six core rope slots at the back are empty. The photo is an homage to this classic AGC photo.

To keep the instruction set and code size small, the AGC had some instructions with side effects you wouldn't expect. For example, the TS (Transfer to Storage) instruction wrote a value to memory, which seems straightforward. But if the previous addition had an overflow (i.e. a carry), TS also skipped the next instruction and loaded the accumulator with a +1 or -1. In other words, simply writing a value to memory could result in a jump in control flow and register modification. The purpose of this was to handle carries for multiple-precision arithmetic, but most computers simply implement this with an "Add with carry" instruction.

Running the program

The video below shows my Bitcoin program running on an actual Apollo Guidance Computer with the results displayed on our DSKY (Display/Keyboard). The DSKY had a simple numeric keypad with buttons large enough for astronauts to use with gloves on. The computer displayed output numerically; astronauts had to know if the output was feet, seconds, degrees, or something else. We used a replica DSKY created by Carl since nobody would let us use a real DSKY.⁸

The Apollo Guidance Computer had a very simple user interface through the DSKY. An astronaut selected an action pressing the "Verb" key, entering a verb number, and pressing "Enter". The astronaut selected a target for the action by entering a "Noun". (Astronauts had a reference card listing all the verbs and nouns.) I added Bitcoin mining as Verb 65 in a program called Borealis⁹; you can see Mike enter Verb 65 at the beginning of the video.

The Apollo Guidance Computer took 5.15 seconds for one SHA-256 hash. Since Bitcoin uses a double-hash, this results in a hash rate of 10.3 seconds per Bitcoin hash. Currently, the Bitcoin network is performing about 65 EH/s (65 quintillion hashes per second). At this difficulty, it would take the AGC 4×10^23 seconds on average to find a block. Since the universe is only 4.3×10^17 seconds old, it would take the AGC about a billion times the age of the universe to successfully mine a block.

Given the astronomical difficulty of mining, you might wonder how I successfully mined a block. For this demonstration, I simply used as input a block that had been successfully mined in the past, specifically block #286819. Thus, the algorithm succeeded quickly, but since it was an old block, I didn't make any money off it.

To put the AGC's mining performance in perspective, a USB stick miner performs 130 billion hashes per second. The stick miner costs under $70, compared to $150,000 for the Apollo Guidance Computer. For its time, the Apollo Guidance Computer was an extremely compact, low-power system, using 55 watts and taking up under a cubic foot of space. The USB miner, though, uses 12 watts and fits in your hand. The enormous difference in performance is due to the exponential increase in computer speed described by Moore's law as well as the advantage of custom Bitcoin mining hardware.

Programming the AGC—then and now

In the 1960s, code for the AGC was written on punch cards, and assembled onto tape using a software system called YUL. This system was more advanced than you'd expect for the 1960s, including a source control system to track and incorporate changes. For flight, the software was woven into core ropes, with wires physically going around cores for a 0 or through cores for a 1. In other words, each core rope was custom-manufactured, with the data stored in the weaving pattern of the wires. This provided high-density, reliable ROM storage, but required weeks of manufacturing.

Detail of core rope memory wiring from an early (Block I) Apollo Guidance Computer. Photo from Raytheon.

Since it wasn't practical to manufacture a new core rope for every change, a different approach was used during development. A core rope simulator allowed a program to be fed into the AGC from external storage. This simulator was part of the refrigerator-sized monitor (below), which provided a debugging interface to the AGC through a test connector on the AGC. The monitor allowed programmers to set breakpoints, single-step, examine registers, and so forth, using lights and switches.

The AGC monitor provided a debugging interface to the AGC as well as a core rope simulator. See User's guide to the AGC monitor.

In my case, I wrote the software on my laptop and assembled it with yaYUL, a modern version of YUL written by the Virtual AGC team. I tested the software on a simulated AGC using the Code::Blocks IDE¹¹, which provides debugging features somewhat similar to what the monitor provided in the 1960s. To run the code on the real AGC, we obviously didn't manufacture core ropes. We have vintage core rope simulator boxes, but they turned out to be extremely unreliable. Fortunately, Mike Stewart built a board to load code into the AGC using the same AGC test connector originally used by the monitor.

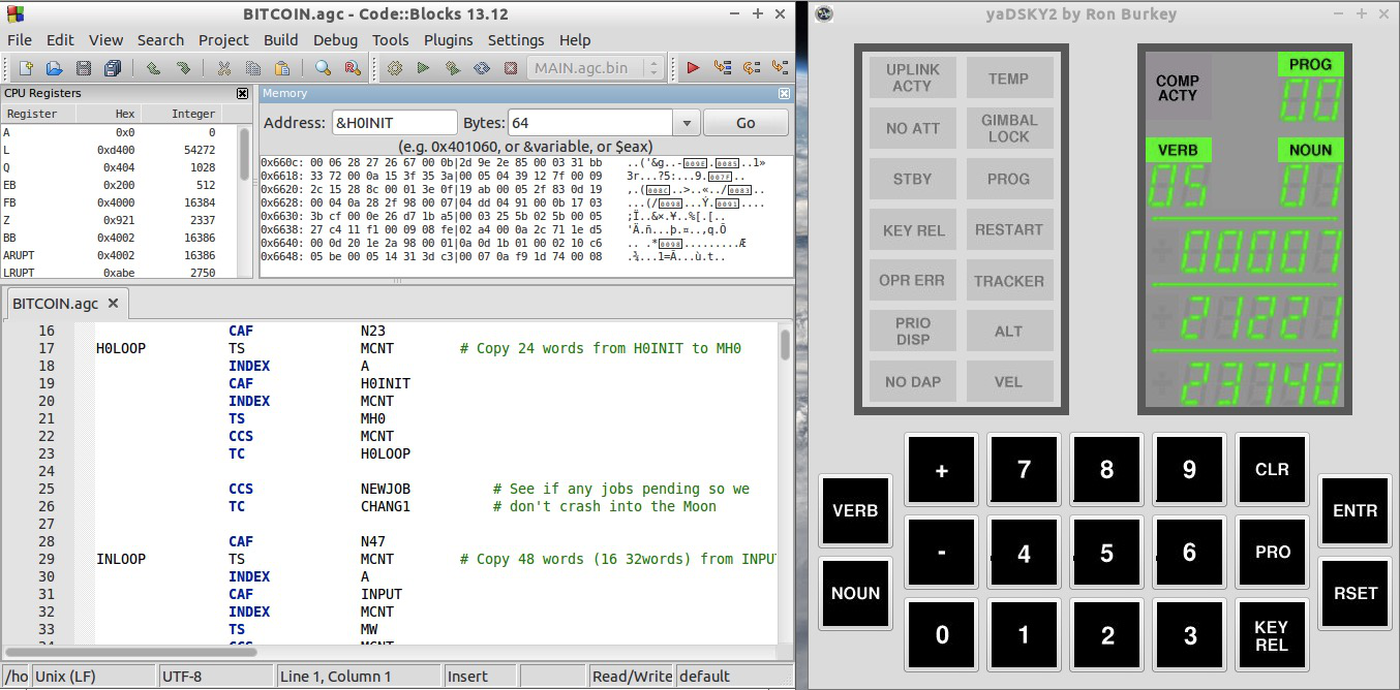AGC code can be developed in an IDE. The debugger makes it much easier to develop code. The IDE communicates with the virtual DSKY.

Conclusion

I implemented the SHA-256 hash algorithm and ran it on the Apollo Guidance Computer that we're restoring, taking 10.3 seconds per hash. This isn't my first experiment with absurd Bitcoin mining. I tried mining by hand with pencil and paper; this had a hash rate of 0.67 hashes per day. Using an IBM punch card mainframe computer from the early 1960s got the hash rate up to 80 seconds per hash. My fastest implementation was on a Xerox Alto (the famous 1973 computer that inspired the Macintosh), which performed 1.5 hashes per second. Thus, the Apollo Guidance Computer outperformed the older transistor-based IBM computer but not the Alto.

My Bitcoin mining experiments by hand, on a punch-card mainframe, and on a Xerox Alto.

The Apollo program cost 25.4 billion dollars as of 1973, equivalent to about 150 billion dollars today. The current market cap of Bitcoin is 200 billion dollars, so if NASA had been mining Bitcoins, they could have paid for the whole Apollo program and still had money left over. One flaw in this plan is the Apollo Guidance Computer's low performance, since mining a block would take much more than the lifetime of the universe.

My code is available on Github; the mining code is in BITCOIN.agc. CuriousMarc has a series of AGC videos which you should watch for more information on the restoration project. I announce my latest blog posts on Twitter, so follow me @kenshirriff for future articles. I also have an RSS feed. Thanks to Mike Stewart for supplying images and extensive information.

Notes and references

1.              The AGC restoration team consists of Mike Stewart (creator of FPGA AGC), Carl Claunch, Marc Verdiell (CuriousMarcon YouTube) and myself. The AGC that we're restoring belongs to a private owner who picked it up at a scrap yard in the 1970s after NASA scrapped it. For simplicity, I refer to the AGC we're restoring as "our AGC".

The Apollo flights had one AGC in the command module (the capsule that returned to Earth) and one AGC in the lunar module. In 1968, before the Moon missions, NASA tested a lunar module with astronauts aboard in a giant vacuum chamber in Houston to ensure that everything worked in space-like conditions. We believe our AGC was installed in that lunar module (LTA-8). Since this AGC was never flown, most of the modules were not potted with epoxy. ↩

2.              Because the AGC supported multiple programs at once, my code needed to periodically call NEWJOB to see if there were any other waiting jobs to run. To ensure reliability, the AGC constantly checked to make sure a faulty program doesn't take over the system. Thus, I needed to give other jobs the chance to run or else my job would get killed. ↩

3.              At the current Bitcoin difficulty level, about 1 in 10^22 hashes will be successful at mining a block; a valid hash must start with approximately 18 zeros. The mining difficulty changes periodically to keep the time between blocks at approximately 10 minutes. As mining hardware gets faster, the difficulty factor is automatically updated to make mining more difficult so miners can never really catch up. ↩

4.              A while back I estimated that Bitcoin mining uses about as much electricity as the entire country of Cambodia. One paperputs mining's energy consumption comparable to Ireland's electricity usage. A recent estimate is that Bitcoin mining uses more electricity than Switzerland. ↩

5.              I've simplified a lot of details in my discussion of Bitcoin algorithms. For in-depth information on Bitcoin and mining, see my articles Bitcoins the hard way and Bitcoin mining the hard way. ↩

6.              Bitcoin uses "double SHA-256" which simply consists of applying the SHA-256 function twice. I could have implemented the double-hash in the AGC code, but I ran out of time; I got the basic hash working at 4 am the night before we sent the AGC back to Houston. How to upload transactions into the AGC is also left as an exercise for the reader. ↩

7.              While SHA-256 is easy to implement, that's not the case for all the cryptography used by Bitcoin. To create a Bitcoin transaction, the transaction must be signed with elliptic curve cryptography. This requires 256-bit modular arithmetic, which is about as hard as it sounds. Even a simple implementation is 1000 lines of C. Needless to say, I decided not to implement signing in assembly language on the AGC. ↩

8.              Many people have asked if we talked to Fran Blanche about the DSKY. Yes, we have. ↩

9.              The Aurora program was used to extensively test the operation of the Apollo Guidance Computer in the Lunar Module. I wrote the Bitcoin code as part of Borealis, a modern version of Aurora slightly cleaned up. The code for Aurora and Borealis includes a table of verb definitions so it was straightforward for me to add Verb 65 for my Bitcoin code. In the video, you can see Mike enter Verb 65 to start the Bitcoin program. I also took advantage of the Executive's octal display routine to show the output. This routine is accessed through Verb 05 Noun 01, which is why you'll see that on the display at the end of the video. ↩

10.          At the end of the video clip, the display shows 8 octal triples indicating the hash: 00000/00000/00000, 00000/00000/00000, 00007/21221/23740, 00017/35565/05002, 00002/20333/04715, 0o00002, 0o33226, 0o05227, 00004/05367/35221, 00005/00252/14222. (The 11111/11111/11111 value is just a signal that all values have been displayed.) Converting these to hex and reversing the bytes yields the 8-byte Bitcoin hash: 00000000 00000000 e067a478 024addfe cdc93628 978aa52d 91fabd42 92982a50. Note the multiple zeros at the beginning of the hash; this is what makes the hash valid. ↩

11.          The Virtual AGC project has developed simulations of the AGC, DSKY, and YUL assembler, so you can experiment with the AGC system. While you can do this from the command line, debugging is much, much easier if you use the Code::Blocks IDE. You can download a VirtualBox environment with everything set up here. In the folder "AGC Visual Debugging", double-click on Borealis to start Code::Blocks. You can edit code in the IDE (or with an editor). Then "Build → Build" compiles the code and "Debug → Start" runs code in the debugger. "Tools → DSKY" starts up a DSKY window to interact with the AGC. "Debug → Debugging windows → Memory dump" lets you look at memory contents. The IDE lets you set breakpoints, single-step through code, examine memory, and so forth. For more information on AGC code development, see this page. ↩

12.          The Bitcoin protocol is a mish-mash of big-endian and little-endian values. It inconveniently reverses the byte order of the SHA-256 hash, so while the hash from the algorithm ends with zeros, the Bitcoin hash starts with zeros. I displayed the hash to match the Bitcoin order. ↩

+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++


- Bloggery committed by chris tower - 1907.09 - 10:10

- Days ago = 1466 days ago

- New note - On 1807.06, I ceased daily transmission of my Hey Mom feature after three years of daily conversations. I plan to continue Hey Mom posts at least twice per week but will continue to post the days since ("Days Ago") count on my blog each day. The blog entry numbering in the title has changed to reflect total Sense of Doubt posts since I began the blog on 0705.04, which include Hey Mom posts, Daily Bowie posts, and Sense of Doubt posts. Hey Mom posts will still be numbered sequentially. New Hey Mom posts will use the same format as all the other Hey Mom posts; all other posts will feature this format seen here.