A Sense of Doubt blog post #1244 - CODING CHALLENGE #2: Swapping Two Variables without a Temp

A Sense of Doubt blog post #1244 -  CODING CHALLENGE #2: Swapping Two Variables without a Temp

Hi everyone!!

Today's subject is coding challenges from the book CRACKING THE CODING INTERVIEW by Gayle Laakmann McDowell.

There's going to be a series of posts as I am working with some folks (one in particular) to hone skills and better understand these types of coding challenges.

Readers will remember that this blog is less about "my teaching" than "my study," and so I am learning and affirming my knowledge base by writing about these subjects.

Also, often, posts like this one get a lot of traffic, I presume, because they show up in people's searches.

But first, this snippet from the book I am reading.

"Arguing with anonymous strangers on the Internet is a sucker's game because they almost always turn out to be -- or to be indistinguishable from -- self-righteous sixteen-year-olds possessing infinite amounts of free time." -- Randy Waterhouse via author Neal Stephenson, Cryptonomicon, pg. 244 (paperback edition)

Often working online and being around the Internet, and yet this prophetic pearl of wisdom was written by Stephenson back in 1999!

I try to avoid putting myself in situations in which I would have to deal with anonymous strangers on the Internet, but I liked this comment for it veracity.

So, the problem.

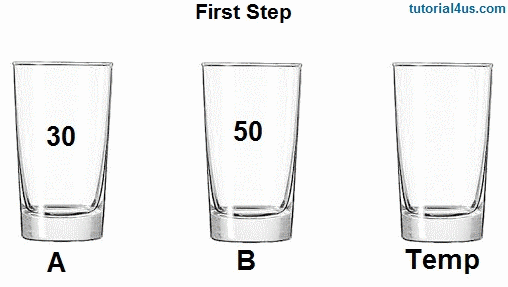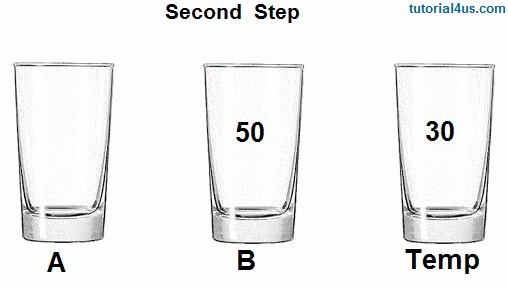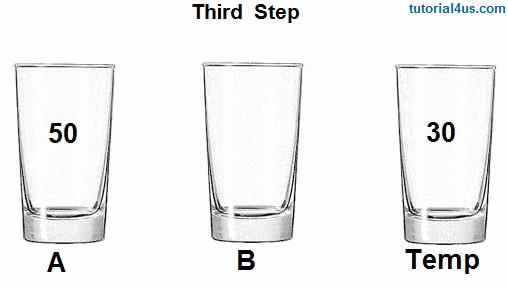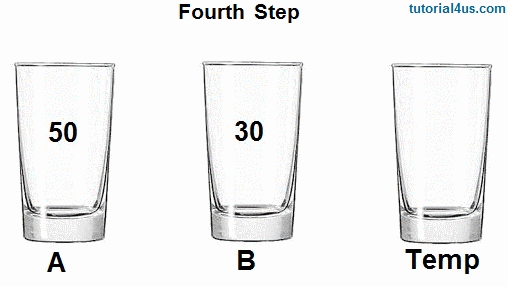
How do you swap two variables in a computer program without using a temp variable?

Because in coding school, (I mean university), we're all taught a function that most of us could think of on our own anyway. Something like this -

def swap(a, b)
       temp = a
       a = b
       b = temp

Pretty basic, right? The main part of the program (often) sends the "swap" function the values "a" and "b," which are probably integers, and there's a third int variable called "temp." In the first line of the function, the variable temp gets the value of the variable of a, then a gets the value of b, which is half of the swap, then b gets the value of temp (which holds a), completing the swap.

For any newbie coders who find my blog entry, temp = a does not really mean temp equals a, so much as it's an assignment statement as I wrote it above: "the variable temp gets the value of the variable of a." When that first statement finished, temp and a are equal because they do hold the same value, though this state changes in the next line.

In this code, the value of a gets saved in the temp variable, so that when a = b overwrites the value in a with the value in b, that's okay and nothing is lost because the "a" value was saved. Then with the value of b safely in the a variable, it can be overwritten with the original value of "a" saved in temp.

See how easy this swap can be performed with a third variable to save a value so nothing is lost when values are overwritten?

So the problem suggests performing this swap WITHOUT a third variable, a "temp" variable.

Say what??

It's a good question because programmers get lazy. The swap function as described is a classic function utility. It's a fundamental concept in programming. In fact, some languages have a built-in swap function already written, so you can just call swap on your variables, and it's done.

As we began to work the problem, I joked that it would be super great if you could swap in one line, something like a=b && b=a or something equally simple.

The day I decided to write this entry and started working on it, I received this tip (below) from Dan Bader's REAL PYTHON site.

See post at - https://www.getdrip.com/deliveries/5yedubbeidmsreisbovq?

# Why Python Is Great: # In-place value swapping # Let's say we want to swap # the values of a and b... a = 23 b = 42 # The "classic" way to do it # with a temporary variable: tmp = a a = b b = tmp # Python also lets us # use this short-hand: a, b = b, a

If you think your friends would find this tip useful, please share it with them—I’d really appreciate it. Here's the link: View in browser To make sure you keep getting these emails, please add info@realpython.com to your address book or whitelist us. Want out of the loop? Unsubscribe. 308 E. 5th Ave, Vancouver BC V5T 1H4

python SWAP under the hood

How great is that?

a, b = b, a 

Now that's an awesome Python trick. Obviously, it's a built-in function. But underneath the hood does the swap happen with a third variable, a temp variable, or does it happen without as in this coding test challenge.

I must admit, at first, I was a bit stumped.

Thankfully, the book provides hints with its challenges. The first hint suggest thinking of the numbers on a number line.

Well, sure. If I could lift both numbers up and flip them, then they would be switched, but I would still need that "space" in which the numbers transition.

Or if I could fold the number line, so the numbers exist at the same point, and then unfold it so that they each return to the other number's point, then the switch could happen that way also.

Neither of these lines of thought led to a coding answer to the problem.

Time for a second hint.

Use the difference between the two numbers and a DIF variable.

Okay, now that's promising, but I am smart enough to know that there's another step because I am introducing a third variable, which eventually I would have to eliminate.

Well... scratch that. I am smart enough to figure this out, but there's a time factor to the figuring out that needs to happen. I don't always SEE the other solution right away. But I am passionate and determined. If you're like me, follow along. We'll get there together.

THAT MAKES A DIFFERENCE!

BUT to get me started, the difference gives me the "distance" between the two numbers.

Let's say a = 7 and b = 5.

Now I can write this.

def swap(a, b)
       dif = a - b
       a = a - dif
       b = b + dif

Okay, not bad. So, first off, we put the difference of a-b (in this case that's the number 2)  in the variable dif. Then a gets the value of itself minus the dif, which in this case is 5, which is the value of b. Again, we're halfway through the swap. Then, conversely, b gets the value of itself PLUS the difference, which in this case is 5 + 2 or 7, the value of a. Swap accomplished!!

Except we have a third variable, and we can't have that.

Still, the hint gets us thinking of using math to solve the problem. So, can we do that same operation, using addition and subtraction, but WITHOUT a third variable.

Well, of course we can because the question would not exist with an answer. So how about this:

def swap(a, b)
       a = a - b
       b = a + b
       a = b - a

So, what does this function do? First off, the variable a gets overwritten with the difference of a and b, which in this case is the number 2. Then b gets the value of the new a, which is 2, added to b, which in this case is 2 + 5 = 7, the original value of a. Now to complete the swap, we simply subtract the "temporary" a value, which is holding the difference between the two numbers, from the new b value, which is the original a value, which should give us the previous b value. In this case, that's 7 - 2 = 5, and so it does.

Wow. Wrapping your mind around how that works?

We simply use one of the variables to store the difference, but since we have the difference, we can get back to both original values of the two numbers with a little addition and subtraction using that difference. That's so cool!!

So why wouldn't we start using this method all the time for swapping? Maybe we will! Saving memory space without declaring a third variable could be useful in a lot of cases.

Now, what if we were asked to do this same operation WITHOUT any math operations?

BITWISE

The following also works, and in so doing, we eliminate the DIF variable but essntially perform a swap the same way with a kind of difference operation on the bit, binary, level.

def swap(a, b)
       a = a ^ b
       b = a ^ b
       a = a ^ b

For newbies, the ^ character denotes the bitwise OR operation.

For those new to bitwise, there's the OR operation and the Exclusive OR operation (XOR). The latter works more like one would intuitively think an OR would work. Usually the bitwise operations are explained using bits, which are defined with 0s and 1s (binary, with me so far?).

For regular OR, one might be looking for a 1, and so when either of the a pair of values holds a 1 -- a = 0, b = 1 (01) or a = 1, b = 0 (10) -- then the OR returns true. But with regular OR, this one is true, too: 11. Only 00 is false in regular OR when looking for 1 to return a true value.  The computer likes when a and b both hold a 1 value because technically speaking a OR b is still 1, so it's true. Regular OR is only false when both values are zeroes because obviously there are no values of 1, and so the condition is not true.

In EXCLUSIVE OR, both 11 and 00 are false in these cases and ONLY 10 or 01 are true, those pairs for which, truly, one OR the other of THE values is a 1 (not both), giving a true result if and only if only one value is a 1 digit and the other a 0.

So in our example, it pretty much works the same way as the difference and sum example. The first line puts a^b in a, which in our example is 2. The second line puts the OR of the new a and b into b, which is now 2 or 5, which results in 7. And then finally, the a variable gets the value of the new a OR the new b, which ORs together 2 or 7, which results in 5.

Here's what the bits look like.

Bit addition and subtraction are explained here with bitwise

https://hackernoon.com/xor-the-magical-bit-wise-operator-24d3012ed821

and here in conceptual terms

https://observablehq.com/@toja/binary-addition-subtraction

If you don't know that 0111 represents a 7 (as I sort of explain below), check this out:

ORIGINALLY
a = 0111 (7 - first position has the one bit turned, then second has a two on, and lastly third position has a 4 activated = 1+2+4 = 7)
b = 0101 (5 - a one and a 4 = 1+4 = 5) (did you get what I mean by 1 for switched on and 0 for off?)

first OR operation (remember this XOR - Exclusive OR)
a = 0111
OR
b = 0101
______
 a = 0010 (2)

second OR operation
a = 0010
OR
b = 0101
______
b = 0111 (7)

third OR operation
a = 0010
OR
b =  0111
______
0101 (5)

Here's notes on the bitwise EXCLUSIVE OR in case you need them.

Bitwise OR |[edit]

bit a	bit b	a | b (a OR b)
0	0	0
0	1	1
1	0	1
1	1	1

Similar to bitwise AND, bitwise OR only operates at the bit level. Its result is a 1 if one of the either bits is 1 and zero only when both bits are 0. Its symbol is | which can be called a pipe.

      11001000  
    | 10111000 
      -------- 
    = 11111000

^[2]

And of course, I am not the first person to write about this issue. As I wrote to start, I am writing this entry as my study, not so much my teaching. I want to make sure I fully understand this process, and I do. Here's some other resources.

https://stackoverflow.com/questions/3647331/how-to-swap-two-numbers-without-using-temp-variables-or-arithmetic-operations

https://www.geeksforgeeks.org/swap-two-numbers-without-using-temporary-variable/

http://code.activestate.com/recipes/579101-swapping-two-variables-without-using-a-third-tempo/

https://medium.com/@frontman/how-swap-two-values-without-temporary-variables-using-javascript-8bb28f96b5f6

Happy coding!!

Crack that coding interview!

+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++


- Bloggery committed by chris tower - 1807.18 - 10:10

- Days ago = 1110 days ago (1110 in binary is 13!! :-))

- New note - On 1807.06, I ceased daily transmission of my Hey Mom feature after three years of daily conversations. I plan to continue Hey Mom posts at least twice per week but will continue to post the days since ("Days Ago") count on my blog each day. The blog entry numbering in the title has changed to reflect total Sense of Doubt posts since I began the blog on 0705.04, which include Hey Mom posts, Daily Bowie posts, and Sense of Doubt posts. Hey Mom posts will still be numbered sequentially. New Hey Mom posts will use the same format as all the other Hey Mom posts; all other posts will feature this format seen here.